Digital Animation in Secondary Math and Science

Create meaningful connections to the curriculum

As digital multimedia tools become more affordable and easy to use, they also become increasingly appropriate for the classroom learning environment. Current research indicates that digital video affords new opportunities for learning, and the professional education associations for science, social studies, mathematics, and English language arts are devoting extensive consideration to the application of digital video technologies to strengthen student learning (Bull and Bell, 2008). Student-created animation is a perfect example of a visual technology that can increase understanding and engage students in the secondary science and mathematics classroom.

In both math and science, students are often asked to remember the steps to complex systems. When students spend their time memorizing answers, rather than understanding and internalizing new material, they are less likely to create links between their prior knowledge and what they are studying. This new “knowledge” is often only short term, likely to be lost or forgotten after the test or quiz has taken place. Digital animation offers an alternative to this process, providing a vehicle for students to create their own meaningful connections with the content. Students who produce their own unique graphics for a mathematical animation are creating their own interactive Visual Mathematical Representations (VMRs), which, in my experience, has a far greater impact on their learning than using pre-existing images to create an animation or watching an existing animation.

When students must simultaneously keep several pieces of information in mind while learning something new, it is advantageous to reduce cognitive load by providing depicted objects and parts of objects proximal to textual discussions (Iding, 2000). Using the drawing tools in Frames, students can produce their own unique computer-based Mathematical Cognitive Tools (MCTs) which support and enhance learning and the cognitive processes of learners (Sedig and Liang, 2006).

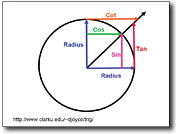
For example, the Unit Circle is the foundation of trigonometry. When students create an animation that contains the basic transcendental functions, they forge their own relationships between the function and its definition. When students animate these graphics for the purpose of describing a mathematical process, they are also creating an artifact that evidences their understanding of the process.

Research indicates that digital animation projects of this nature can have truly compelling results. Developing original illustrated animations provides a rare opportunity to enrich the curriculum using students’ own creativity. My colleagues and I have noticed increased engagement as students create their own learning objects and take ownership of the material they are learning.

In the animation design process, the Frames drawing tools help students simplify a complex tasks. For example, in the case of cell division, a student can begin by illustrating a cell, and then duplicate the frame, making minor changes to the chromosomes as the cell divides. Duplicating frames in this fashion reduces cognitive load, allowing students to focus their attention of the actual process of cell division. Mayer and colleagues have promoted a generative theory of multimedia design, suggesting that the selection, organization, and integration of to-be-learned information are of benefit in designed instruction (Mayer and Moreno, 2002).

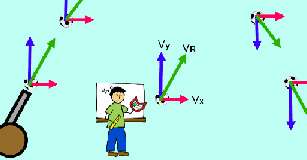
Projectile motion is a fundamental physics concept that describes how objects fall freely under the effects of gravity. Using digital animation tools to describe projectile motion gives students the opportunity to integrate their understanding of two significant mathematical concepts, vector addition and parabolic functions, with their understanding of free-fall. In doing so, students work to overcome any existing misconceptions, ultimately developing a better understanding of the physical system.

Research into cognitive processes has shown that learning is most effective when the learning environment includes four core conditions: active engagement, participation in groups, frequent interaction and feedback, and connections to real-world contexts (Roschelle, Pea, Hoadly, Gordon, and Means, 2000). Using Frames to create digital animations allows you to integrate all four conditions in your math and science classroom. As students create animations, they also develop their own processes by which they solve an essential question posed by their teacher. This creative freedom allows students to produce an animation that is authentic, relevant, more meaningful.

Geometry is another arena where digital animation can contribute to engagement and understanding. Geometric proofs build the foundation upon which most geometric principals are based. Many students find proofs complicated and difficult to complete. To animate a proof successfully, students must reduce it to individual elements in order to depict visually the necessary connections between each one.

Students are led to develop strategies for solving problems using the software, developing their geometrical thinking as they combine activities with the questions asked during the animation process (Patsiomitou, 2008). The statements in a two column proof act as guiding questions throughout the development of a complete proof. These statements can also serve as a storyboard for development, with the steps of the proof playing out the solution during the final animation.

Integrating animation into your science and math classrooms allows you to engage the boundless creativity each of your students possesses. When you put digital animation tools into the hands of students, you provide them the opportunity to construct their own projects and build their own understanding.

Bibilography

Roschelle, J.M., Pea, R.D., Hoadley, C.M., Gordon, D.N., and Means, B.M. (2000). Changing how and what children learn in school with computer-based technologies. Children and Computer Technology, 10(2), 76-101.

Sedig, K. and Liang, H.N. (2006). Interactivity of visual mathematical representations: Factors affecting learning and cognitive processes. Journal of Interactive Learning Research, 17(2), 179-212.

Bull, G., and Bell, L. (July 2008). Lights, camera, learning! Learning & Leading with Technology, 36 (8), 30-31.

Iding, M.K. (2000). “Is seeing believing? Features of effective multimedia for learning science.” International Journal of Instructional Media, 27(4), 403.

Mayer, R., and Moreno, R. (2002). Animation as an aid to multimedia learning. Educational Psychology Review, 14(1), 87-99.

Patsiomitou, S. (2008). The development of students geometrical thinking through transformational processes and interaction techniques in a dynamic geometry environment. Issues in Informing Science and Information Technology, 5, 353-393.

by Brad Smrstick

Brad Smrstick is a former high school math and science teacher with more than 20 years of experience in the classroom teaching physics across all levels from conceptual to A.P. He has participated in summer research programs at the FermiLab, Lawrence Livermore National Laboratory, the University of Florida, and the University of South Florida. He now applies his craft as team lead for Technology Training at Staff Development in Hillsborough County, Florida.